Okabe and El Psy Kongroo

题目描述

你在 $(0,0)$ 。

在 $(x,y)$ 时，每次移动可以到达 $(x+1,y+1),(x+1,y),(x+1,y-1)$ 。

平面上有 $n$ 条线段，平行于 $x$ 轴，参数为$a_i$ , $b_i$ ,$c_i$ ，表示在 $(a_i,c_i)$ 到 $(b_i,c_i)$ 的一条线段，保证 $b_i=a_{i+1}$。

要求你一直在线段的下方且在 $x$ 轴上方，即 $a_i \leq x \leq b_i$ 时， $0 \leq y \leq c_i$ 。

问 $:$ 到达 $(k,0)$ 的方案数，方案数对 $10^9+7$ 取模。

$n \leq 100 , k \leq 10^{18} , c_i \leq 15$

输入格式

第一行包含整数 $n$ 和 $k$ ( $ 1 \leq n \leq 100 $ , $ 1 \leq k \leq 10^{18} $ ), 表示线段数和终点的横坐标

下面 $n$ 行每行包含三个整数 $ a_{i} $ , $ b_{i} $ , $ c_{i} $ ( $ 0\leq a_{i}\leq b_{i}\leq 10^{18} $ , $ 0 \leq c_{i} \leq 15 $ ), 表示每个线段的左端点, 右端点, 和它的纵坐标

保证 $ a_{1}=0 $ , $ a_{n} \leq k \leq b_{n} $ , $ a_{i}=b_{i-1} $.

输出格式

问 $:$ 到达 $(k,0)$ 的方案数，方案数对 $10^9+7$ 取模。

样例 #1

样例输入 #1

样例输出 #1

1
4

样例 #2

样例输入 #2

样例输出 #2

1
4

提示

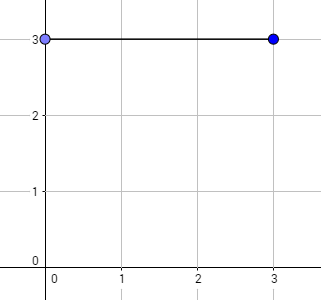
The graph above corresponds to sample 1. The possible walks are:

$$ (0, 0) \rightarrow (1, 0) \rightarrow (2, 0) \rightarrow (3, 0) $$ $$ (0, 0) \rightarrow (1, 1) \rightarrow (2, 0) \rightarrow (3, 0) $$ $$ (0, 0) \rightarrow (1, 0) \rightarrow (2, 1) \rightarrow (3, 0) $$ $$ (0, 0) \rightarrow (1, 1) \rightarrow (2, 1) \rightarrow (3, 0) $$

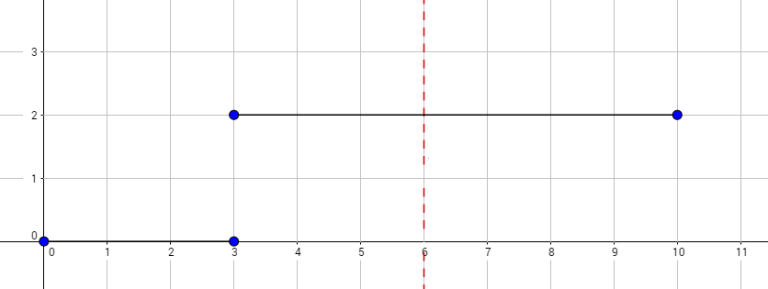
The graph above corresponds to sample 2. There is only one walk for Okabe to reach $ (3,0) $ . After this, the possible walks are:

$$ (3, 0) \rightarrow (4, 0) \rightarrow (5, 0) \rightarrow (6, 0) $$ $$ (3, 0) \rightarrow (4, 0) \rightarrow (5, 1) \rightarrow (6, 0) $$ $$ (3, 0) \rightarrow (4, 1) \rightarrow (5, 0) \rightarrow (6, 0) $$ $$ (3, 0) \rightarrow (4, 1) \rightarrow (5, 1) \rightarrow (6, 0) $$

题解

本题递推方程

$$ dp_{x,y} = dp_{x-1, y-1} + dp_{x-1, y} + d_{x-1, +y1} $$

然而 $k$ 的范围是 $ 1 \leq k \leq 10^{18} $, 递推会 TLE ! 所以很容易想到要用矩阵加速递推

对所有 $x$, 列出所有 $y \in [0, c_i]$ 的递推关系 $:$

$$ dp_{x, 0} = dp_{x-1, 0} + dp_{x-1, 1} \newline dp_{x, 1} = dp_{x-1, 0} + dp_{x-1, 1} + dp_{x-1, 1} \newline dp_{x, 2} = dp_{x-1, 1} + dp_{x-1, 2} + dp_{x-1, 3} \newline \vdots \newline dp_{x, c_i-1} = dp_{x-1, c_i-2} + dp_{x-1, c_i-1} + dp_{x-1, c_i} \newline dp_{x, c_i} = dp_{x-1, c_i-1} + dp_{x-1, c_i} $$

写出其矩阵形式

$$ \begin{bmatrix} dp_{x, 0} \newline dp_{x, 1} \newline dp_{x, 2} \newline dp_{x, 3} \newline dp_{x, 4} \newline \vdots \newline dp_{x, c_i-2} \newline dp_{x, c_i-1} \newline dp_{x, c_i} \end{bmatrix} = \begin{bmatrix} \textcolor{red}{1} & \textcolor{red}{1} & 0 & 0 & \cdots & 0 & 0 & 0 & 0 \newline \textcolor{red}{1} & \textcolor{red}{1} & \textcolor{red}{1} & 0 & \cdots & 0 & 0 & 0 & 0 \newline 0 & \textcolor{red}{1} & \textcolor{red}{1} & \textcolor{red}{1} & \cdots & 0 & 0 & 0 & 0 \newline 0 & 0 & \textcolor{red}{1} & \textcolor{red}{1} & \cdots & 0 & 0 & 0 & 0 \newline 0 & 0 & 0 & \textcolor{red}{1} & \cdots & 0 & 0 & 0 & 0 \newline \vdots & \vdots & \vdots & \vdots & \ddots & \vdots & \vdots & \vdots & \vdots & \newline 0 & 0 & 0 & 0 & \cdots & \textcolor{red}{1} & \textcolor{red}{1} & 0 & 0 \newline 0 & 0 & 0 & 0 & \cdots & \textcolor{red}{1} & \textcolor{red}{1} & \textcolor{red}{1} & 0 \newline 0 & 0 & 0 & 0 & \cdots & 0 & \textcolor{red}{1} & \textcolor{red}{1} & \textcolor{red}{1} \newline \end{bmatrix} \begin{bmatrix} dp_{x-1, 0} \newline dp_{x-1, 1} \newline dp_{x-1, 2} \newline dp_{x-1, 3} \newline dp_{x-1, 4} \newline \vdots \newline dp_{x-1, c_i-2} \newline dp_{x-1, c_i-1} \newline dp_{x-1, c_i} \end{bmatrix} $$

其中, 第二个矩阵大小为 $(c_i+1) * (c_i+1)$

所以, 对 $\forall i \in [1, n]$, 都有

$$ \begin{bmatrix} dp_{b_i, 0} \newline dp_{b_i, 1} \newline dp_{b_i, 2} \newline dp_{b_i, 3} \newline dp_{b_i, 4} \newline \vdots \newline dp_{b_i, c_i-2} \newline dp_{b_i, c_i-1} \newline dp_{b_i, c_i} \end{bmatrix} = \begin{bmatrix} \textcolor{red}{1} & \textcolor{red}{1} & 0 & 0 & \cdots & 0 & 0 & 0 & 0 \newline \textcolor{red}{1} & \textcolor{red}{1} & \textcolor{red}{1} & 0 & \cdots & 0 & 0 & 0 & 0 \newline 0 & \textcolor{red}{1} & \textcolor{red}{1} & \textcolor{red}{1} & \cdots & 0 & 0 & 0 & 0 \newline 0 & 0 & \textcolor{red}{1} & \textcolor{red}{1} & \cdots & 0 & 0 & 0 & 0 \newline 0 & 0 & 0 & \textcolor{red}{1} & \cdots & 0 & 0 & 0 & 0 \newline \vdots & \vdots & \vdots & \vdots & \ddots & \vdots & \vdots & \vdots & \vdots & \newline 0 & 0 & 0 & 0 & \cdots & \textcolor{red}{1} & \textcolor{red}{1} & 0 & 0 \newline 0 & 0 & 0 & 0 & \cdots & \textcolor{red}{1} & \textcolor{red}{1} & \textcolor{red}{1} & 0 \newline 0 & 0 & 0 & 0 & \cdots & 0 & \textcolor{red}{1} & \textcolor{red}{1} & \textcolor{red}{1} \newline \end{bmatrix} ^ {b_i - a_i} \begin{bmatrix} dp_{a_i-1, 0} \newline dp_{a_i-1, 1} \newline dp_{a_i-1, 2} \newline dp_{a_i-1, 3} \newline dp_{a_i-1, 4} \newline \vdots \newline dp_{a_i-1, c_i-2} \newline dp_{a_i-1, c_i-1} \newline dp_{a_i-1, c_i} \end{bmatrix} $$

所以只要记录对 $ \forall i \in [1, n-1]$ 进行矩阵快速幂后的结果, 存储在 $base$ 中, 在第 $i+1$ 次循环中使用, 答案即为结果矩阵的第一个数字

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef double db;
typedef pair<int, int> pii;
typedef pair<long long, long long> pll;
typedef vector<int> vi;
typedef vector<long long> vll;
typedef vector<pii> vpii;
typedef vector<pll> vpll;

const int N = 1000010, MOD = 1e9 + 7, INF = 0x3f3f3f3f;
typedef vector<vector<ll>> mat;
int T, n, c;
ll k, a, b;

mat mul(mat A, mat B) {
    int n = (int)A.size(), p = (int)A[0].size(), m = (int)B[0].size();
    mat C(n, vll(m));
    for (int k = 0; k < p; k++)
        for (int i = 0; i < n; i++)
            for (int j = 0; j < m; j++)
                C[i][j] = (C[i][j] + A[i][k] * B[k][j]) % MOD;
    return C;
}
mat qpow(mat A, ll m) {
    int n = (int)A.size();
    mat B(n, vll(n));
    for (int i = 0; i < n; i++) B[i][i] = 1;
    while (m) {
        if (m & 1) B = mul(B, A);
        A = mul(A, A);
        m >>= 1;
    }
    return B;
}

int main() {
#ifndef ONLINE_JUDGE
    freopen("data/in.txt", "r", stdin);
    freopen("data/out.txt", "w", stdout);
#endif
    ios::sync_with_stdio(false);
    cin >> n >> k;
    mat base;
    for (int i = 1; i <= n; i++) {
        cin >> a >> b >> c;
        if (i == 1) {
            base = mat(c + 1, vll(1));
            base[0][0] = 1;
        } else {
            while (base.size() < c + 1) base.push_back(vll(1));
        }
        mat ma = mat(c + 1, vll(c + 1));
        for (int j = 0; j <= c; j++) {
            for (int k = max(0, j - 1); k <= min(c, j + 1); k++) {
                ma[j][k] = 1;
            }
        }
        base = mul(qpow(ma, min(b, k) - a), base);
    }
    cout << base[0][0] << "\n";
    return 0;
}