[ZJOI2006]三色二叉树

题目描述

一棵二叉树可以按照如下规则表示成一个由 $0$、$1$、$2$ 组成的字符序列，我们称之为“二叉树序列 $S$”：

$$S= \begin{cases} 0& \text 表示该树没有子节点 \newline 1S_1& 表示该树有一个节点，S_1 为其子树的二叉树序列 \newline 2S_1S_2& 表示该树由两个子节点，S_1 和 S_2 分别表示其两个子树的二叉树序列 \end{cases}$$

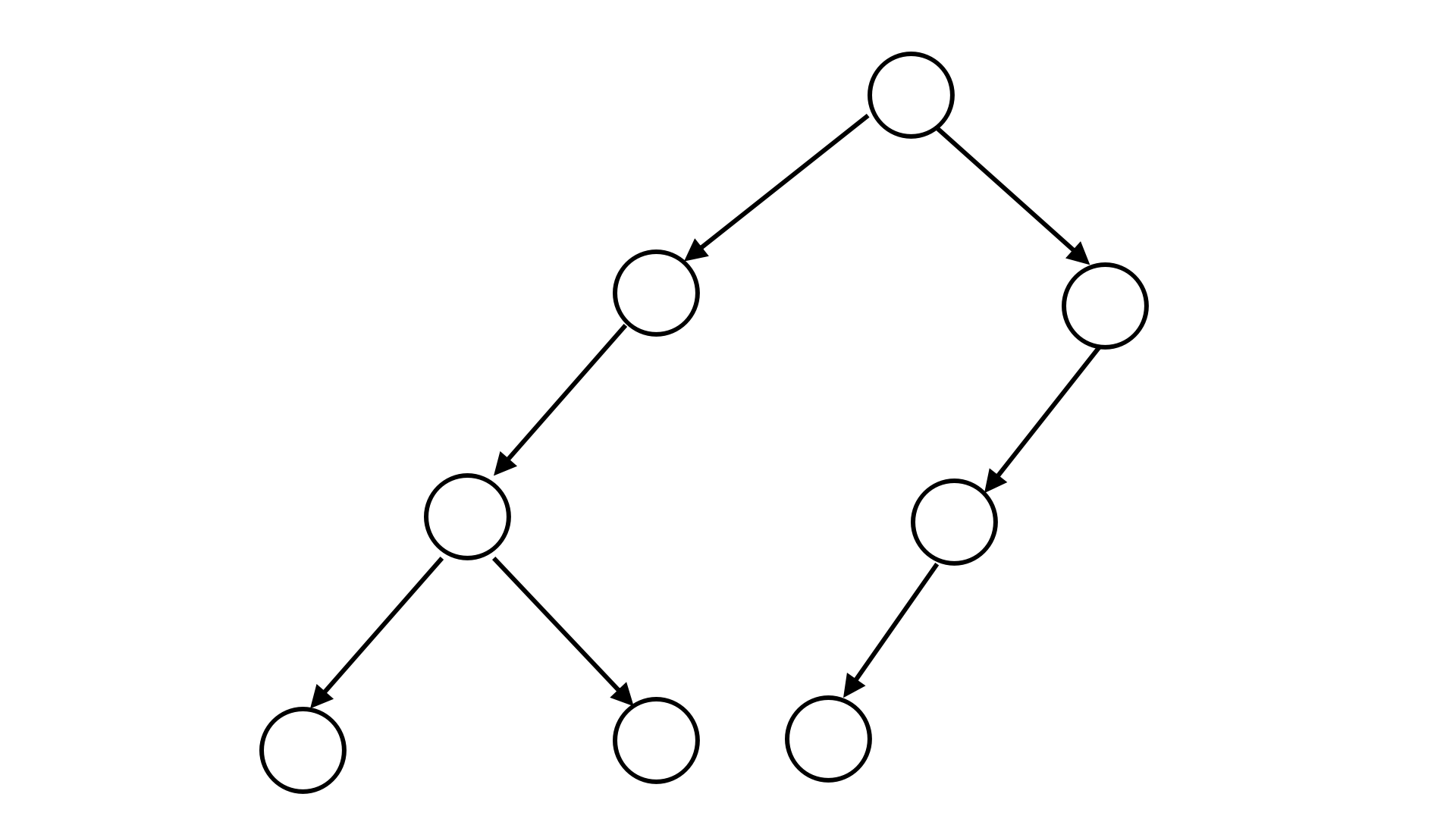
例如，下图所表示的二叉树可以用二叉树序列 $S=\texttt{21200110}$ 来表示。

你的任务是要对一棵二叉树的节点进行染色。每个节点可以被染成红色、绿色或蓝色。并且，一个节点与其子节点的颜色必须不同，如果该节点有两个子节点，那么这两个子节点的颜色也必须不同。给定一颗二叉树的二叉树序列，请求出这棵树中最多和最少有多少个点能够被染成绿色。

输入格式

输入只有一行一个字符串 $s$，表示二叉树序列。

输出格式

输出只有一行，包含两个数，依次表示最多和最少有多少个点能够被染成绿色。

样例 #1

样例输入 #1

1
1122002010

样例输出 #1

1
5 2

数据规模与约定

对于全部的测试点，保证 $1 \leq |s| \leq 5 \times 10^5$，$s$ 中只含字符 0 1 2。

题解

本题是一道 ~~非常简单的树形DP模板题~~

定义 $ dp_{r, c} $ 表示 $:$ 结点 $r$ 涂上颜色 $c \text{(绿色: 0, 红色: 1, 蓝色: 2)} $ 时, $r$的子树最多有多少个点能够被染成绿色

状态转移方程

$$ \begin{equation} dp_{r, 0} = \begin{cases} max(dp_{ls, 1} + dp_{rs, 2}, dp_{ls, 2} + dp_{rs, 1}) + 1, \text{$r$ 不为叶节点} \newline 1, \text{$r$ 为叶节点} \end{cases} \end{equation} $$

$$ \begin{equation} dp_{r, 1} = \begin{cases} max(dp_{ls, 0} + dp_{rs, 2}, dp_{ls, 2} + dp_{rs, 0}), \text{$r$ 不为叶节点} \newline 0, \text{$r$ 为叶节点} \end{cases} \end{equation} $$

$$ \begin{equation} dp_{r, 2} = \begin{cases} max(dp_{ls, 1} + dp_{rs, 2}, dp_{ls, 2} + dp_{rs, 1}), \text{$r$ 不为叶节点} \newline 0, \text{$r$ 为叶节点} \end{cases} \end{equation} $$

$$ \text{最小值同理} $$

由叶节点开始 dp, 结果即为 $ max(dp_{root, 0}, dp_{root, 1}, dp_{root, 2}) $

可以在 dfs 时进行 dp, 也可以先把树建好再 dp, 标程使用的是的二种方法

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef double db;
typedef pair<int, int> pii;
typedef pair<long long, long long> pll;
typedef vector<int> vi;
typedef vector<long long> vll;
typedef vector<pii> vpii;
typedef vector<pll> vpll;

const int N = 500010, MOD = 1e9 + 7, INF = 0x3f3f3f3f;
int n, dpmax[N][5], dpmin[N][5];
string s;
struct Node {
    int l, r;
} a[N];

int build(int x) {
    int len = 0;
    if (s[x] == '2') {
        a[x + 1].l = x + 2;
        int l1 = build(x + 1);
        a[x + 1].r = x + l1 + 2;
        int l2 = build(x + l1 + 1);
        len += l1 + l2;
    } else if (s[x] == '1') {
        a[x + 1].l = x + 2;
        int l = build(x + 1);
        len += l;
    } else if (s[x] == '0')
        return 1;
    return len + 1;
}

void dfs(int x) {
    if (a[x].l == 0 && a[x].r == 0)
        dpmax[x][0] = dpmin[x][0] = 1,
        dpmax[x][1] = dpmax[x][2] = dpmin[x][1] = dpmin[x][2] = 0;
    if (a[x].l) dfs(a[x].l);
    if (a[x].r) dfs(a[x].r);
    dpmax[x][0] = max(dpmax[a[x].l][1] + dpmax[a[x].r][2],
                      dpmax[a[x].l][2] + dpmax[a[x].r][1]) +
                  1;
    dpmax[x][1] = max(dpmax[a[x].l][0] + dpmax[a[x].r][2],
                      dpmax[a[x].l][2] + dpmax[a[x].r][0]);
    dpmax[x][2] = max(dpmax[a[x].l][0] + dpmax[a[x].r][1],
                      dpmax[a[x].l][1] + dpmax[a[x].r][0]);
    dpmin[x][0] = min(dpmin[a[x].l][1] + dpmin[a[x].r][2],
                      dpmin[a[x].l][2] + dpmin[a[x].r][1]) +
                  1;
    dpmin[x][1] = min(dpmin[a[x].l][0] + dpmin[a[x].r][2],
                      dpmin[a[x].l][2] + dpmin[a[x].r][0]);
    dpmin[x][2] = min(dpmin[a[x].l][0] + dpmin[a[x].r][1],
                      dpmin[a[x].l][1] + dpmin[a[x].r][0]);
}

int main() {
#ifndef ONLINE_JUDGE
    freopen("data/in.txt", "r", stdin);
    freopen("data/out.txt", "w", stdout);
#endif
    ios::sync_with_stdio(false);
    cin >> s;
    n = s.size();
    build(0);
    dfs(1);
    cout << max(dpmax[1][0], max(dpmax[1][1], dpmax[1][2])) << " "
         << min(dpmin[1][0], min(dpmin[1][1], dpmin[1][2]));
    return 0;
}