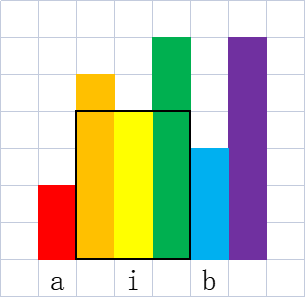最大正方形

题目描述

在一个 n*m 的只包含 0 和 1 的矩阵里找出一个不包含 0 的最大正方形，输出边长。

输入格式

输入文件第一行为两个整数 n,m（1<=n,m<=100），接下来 n 行，每行 m 个数字，用空格隔开，0 或 1.

输出格式

一个整数，最大正方形的边长

样例 #1

样例输入 #1

样例输出 #1

1
2

题解

引入

首先, 想一道类似的题

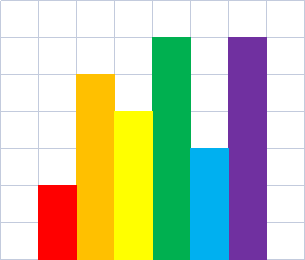
有 $n$ 个长为 $h_i$, 宽为 $1$ 的小矩形并排摆放, 求能从中间找出的最大矩形

例如, $h = {2, 5, 4, 6, 3, 6}$

对于每一个 $i$, 找到 $:$

最大的 $a \lt i$, 使得 $h_a < h_i$
最小的 $b \gt i$, 使得 $h_b < h_i$

$b - a - 1$ 就是包含第 $i$ 个矩形的长(或宽)

以 $i = 3$ 时为例, 此时 $j = 1, k = 5$

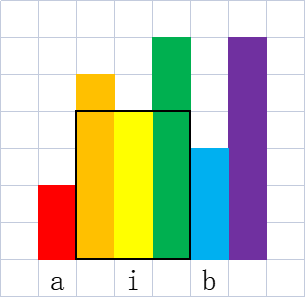
若要求最大正方形, 答案为 $min(h_i , j - k - 1)$

真·题解 😎

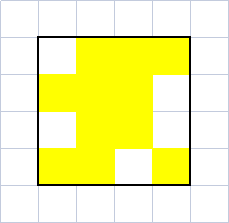
以样例为例, 黄色表示 $1$, 白色表示 $0$

假设以第 $2$ 行为正方形底边, 统计出第 $2$ 行上方黄块的数量, 画出下面一张图

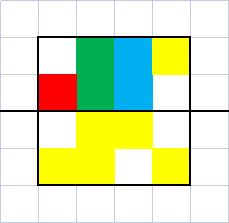
这就和一开始引入中讲的一样:

对于每一个 $j$, 找到 $:$

最大的 $a \lt j$, 使得 $h_a < h_j$
最小的 $b \gt j$, 使得 $h_b < h_j$

以第 $i$ 行为底边的正方形边长最大为 $\max \limits_{j = 1}^{m}{min(b-a-1, h_j)}$

所以解题步骤如下

枚举正方形底边($1$ ~ $n$), 同时维护 $h$ 数组
用单调栈(递增)求出最大的 $a \lt j$, 使得 $h_a < h_j$
用单调栈(递增)求出最小的 $b \gt j$, 使得 $h_b < h_j$

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef double db;
typedef pair<int, int> pii;
typedef pair<long long, long long> pll;
typedef vector<int> vi;
typedef vector<long long> vll;
typedef vector<pii> vpii;
typedef vector<pll> vpll;

const int N = 110, MOD = 1e9 + 7, INF = 0x3f3f3f3f;
int n, m, a[N][N], s[N], top, h[N], l[N], r[N], ans;

int main() {
#ifndef ONLINE_JUDGE
    freopen("data/in.txt", "r", stdin);
    freopen("data/out.txt", "w", stdout);
#endif
    cin >> n >> m;
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= m; j++) cin >> a[i][j];
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= m; j++) {
            if (a[i][j])
                h[j]++;
            else
                h[j] = 0;
        }

        top = 0;
        s[++top] = 0;
        for (int j = 1; j <= m; j++) {
            while (top > 0 && h[s[top]] >= h[j]) top--;
            l[j] = s[top];
            s[++top] = j;
        }

        top = 0;
        s[++top] = m + 1;
        for (int j = m; j >= 1; j--) {
            while (top > 0 && h[s[top]] >= h[j]) top--;
            r[j] = s[top];
            s[++top] = j;

            ans = max(ans, min(r[j] - l[j] - 1, h[j]));
        }
    }
    cout << ans;
    return 0;
}